L’exactitude des prévisions de la demande pour le plan industriel et commercial (PIC/S&OP) est extrêmement importante et fondamentale pour son succès au sein d’une entreprise. Certaines lacunes des méthodes de prévision basiques peuvent nuire à la crédibilité de votre PIC.
Dans cet article, nous expliquerons comment résoudre certains problèmes associés au modèle de lissage exponentiel simple. Comme indiqué dans un précédent article de blog, ce modèle crée une prévision simple qui suppose que la série chronologique de la demande future est similaire à son passé. Un problème majeur avec ce lissage simple est son incapacité à identifier et à projeter une tendance.
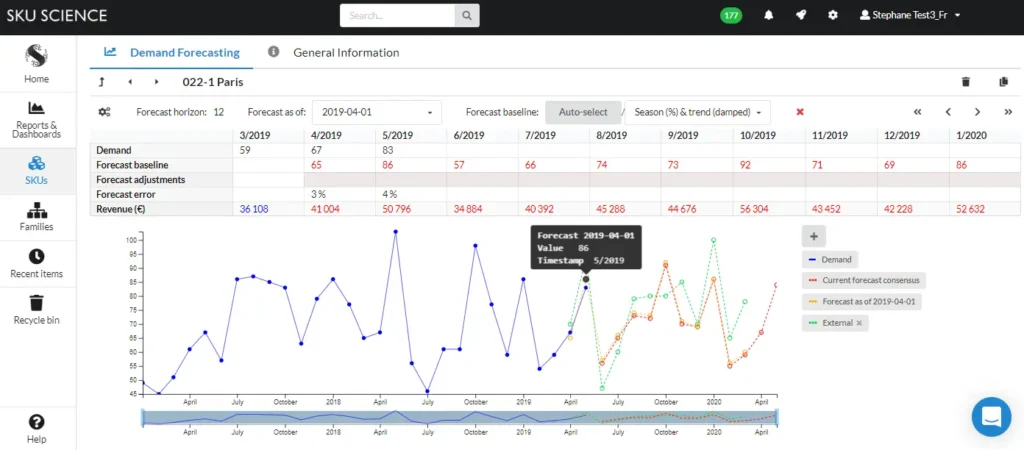
Essayez notre solution de prévision simple & rapide !
Inscrivez-vous aujourd’hui gratuitement sur SKU Science
Données d’échantillon préchargées – Aucune carte de crédit requise
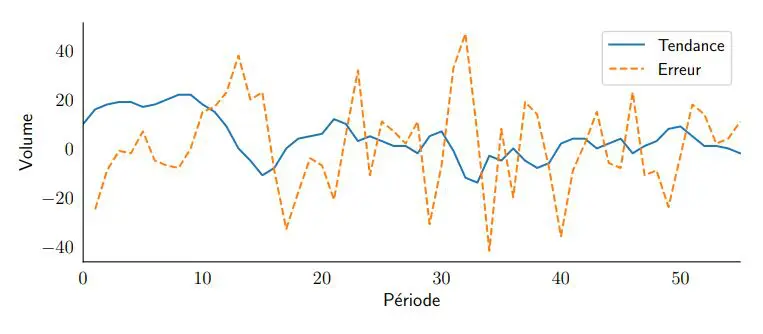
Nous définissons la tendance comme la variation moyenne du niveau de série temporelle entre deux périodes consécutives . Dans notre article précédent, nous définissions le niveau comme la valeur moyenne autour de laquelle la demande varie dans le temps. Ainsi, par exemple, si vous aviez un niveau de vente la semaine dernière de 10 pièces et que cette semaine le niveau des ventes est d'environ 20 pièces, cela signifie que vous avez une tendance positive de 10 pièces par semaine.
Si vous supposez que votre série chronologique suit une tendance, vous ne connaîtrez probablement pas son amplitude à l’avance; d'autant plus que cette ampleur peut varier dans le temps. Cependant, il existe maintenant un modèle qui permet de distinguer par lui-même la tendance dans le temps. Comme on le voit pour le niveau, ce nouveau modèle estimera la tendance sur la base d’un nouveau paramètre d’apprentissage appelé beta (
), donnant plus ou moins d’importance aux observations les plus récentes. Rappelez-vous que alpha (
) déterminera l’importance accordée à la dernière observation de la demande.
Ces techniques de prévision de la demande sont maintenant entièrement disponibles sur SKU Science, et nous expliquons ci-dessous certains de leurs concepts clés.
Explications rapides sur la méthode de prévision de la demande à lissage exponentiel double
L'idée générale des modèles à lissage exponentiel double est que le niveau et la tendance seront mis à jour à chaque période sur la base de l'observation la plus récente et de l'estimation précédente de chaque composante.
Comme vous vous en souviendrez peut-être, avec le modèle de lissage exponentiel simple, nous avons mis à jour les prévisions pour chaque période, en partie en fonction de la demande précédente et en partie en fonction des prévisions précédentes.
Nous allons maintenant faire la même chose pour le niveau (
) et la tendance (
).
Notre nouveau modèle de prévision de la demande mettra à jour son estimation du niveau à chaque période grâce à deux informations: la dernière observation de la demande et l'estimation du niveau précédent augmentées de la tendance.
Ce modèle de prévision de la demande devra également estimer la tendance. Tout comme pour le niveau, elle représente le poids accordé à l'observation de niveau la plus récente.
Dès que nous sommes sortis de la période de demande historique, nous prévoyons simplement chaque période comme la dernière prévision plus la tendance. Le modèle extrapolera donc la dernière tendance observée. Cependant, comme nous le verrons plus tard, cela pourrait poser un problème.
Vous pouvez voir ci-dessous la représentation mathématique de la technique de prévision:
- Estimation de niveau:
- Estimation de tendance:
- Prévisions futures:
Initialisation de notre modèle de prévision de la demande
Comme nous l’avons vu avec l’initialisation prévue du lissage exponentiel simple, nous devons examiner comment initialiser les premières estimations de notre niveau et de notre tendance, et nous aurons deux options, décrites ci-dessous.
- Initialization simple
Nous pouvons initialiser le niveau et la tendance simplement en prenant 
and 
. C'est une méthode d'initialisation simple et juste.
- Régression linéaire
Une autre façon d’initialiser 
et 
serait de faire une régression linéaire des n premières observations de la demande, qui pourrait être définie comme un nombre arbitrairement bas (par exemple 3 ou 5). Nous ne traiterons pas dans cet article de comment faire des régressions linéaires.
Compréhension de ces modèles de prévision de la demande
Les modèles de lissage exponentiels sont très utiles car ils permettent de comprendre une prévision ou une série chronologique grâce à leur décomposition entre le niveau et la tendance et (comme nous le verrons dans un autre article de ce blog), la saisonnalité . Vous pouvez vérifier l'état de n'importe lequel des sous-composants de la demande à tout moment, tout comme vous pourriez vérifier ce qui se passe sous le capot d'une voiture. il n'en va pas de même avec un algorithme à base d'intelligence artificielle.
Dans l'exemple ci-dessous, nous avons tracé ces différents composants pour vous montrer comment notre modèle interprète l'évolution de la courbe de demande d'un produit. Nous sommes ainsi capable d'expliquer la valeur de chaque point de prévision.
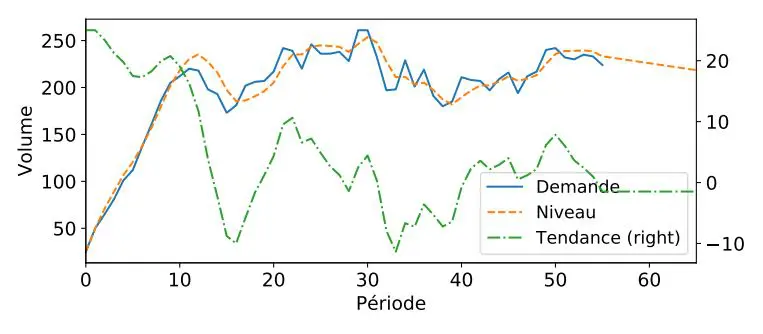
La valeur des différents paramètres de lissage vous indiquera également quelque chose sur la variabilité ou la régularité de votre produit. Les valeurs élevées désigneront un produit où chaque variation devrait avoir un impact sur les prévisions; les valeurs faibles désigneront des produits ayant un comportement plus constant et qui ne devraient pas être affectés par des fluctuations à court terme.
Limites du modèle de prévision de la demande à lissage exponentiel double
Notre modèle à lissage exponentiel double est maintenant capable de reconnaître une tendance et de l'extrapoler dans le futur. C'est une amélioration majeure par rapport au lissage exponentiel simple ou à la moyenne mobile. Malheureusement, cela comporte un risque.
Notre modèle suppose que la tendance se poursuivra éternellement. Cela pourrait entraîner des problèmes pour les prévisions à moyen / long terme. Nous allons résoudre ce problème grâce au modèle de tendance amorti, un modèle publié il y a 25 ans, en 1985!
Outre le risque de tendance infinie, nous avons encore
- Le manque de saisonnalité. Ce problème sera résolu via le modèle de lissage triple exponentiel détaillé dans notre prochain article de blog.
- L'impossibilité de prendre en compte des informations externes (telles que le budget marketing ou les variations de prix).
Améliorer la technique de prévision avec une tendance amortie
Pour résoudre une partie de ces limitations, Gardner et McKenzie (1985) ont proposé d'ajouter une nouvelle couche d'intelligence: un facteur d'amortissement phi (
) qui réduira de manière exponentielle la tendance au fil du temps. Par conséquent, notre modèle ne retiendra qu'une fraction de la tendance estimée précédente.
Ce facteur d’amortissement peut sembler à première vue une idée simple, mais en réalité, il nous permet d’être beaucoup plus précis pour les prévisions à moyen et à long terme. Néanmoins, notre modèle doit encore être capable de reconnaître un schéma saisonnier pouvant être appliqué aux prévisions futures. De nombreuses chaînes logistiques sont confrontées à la saisonnalité d'une manière ou d'une autre. Nous avons donc besoin que nos modèles de prévision soient suffisamment intelligents pour planifier ces modèles. Pour ce faire, nous décrirons une troisième couche de lissage exponentiel dans les articles à suivre .
Référence bibliographique: “Data Science for Supply Chain Forecast – Nicolas Vandeput”
Vous pouvez également voir une analyse plus détaillée des deux modèles (lissage double et lissage amorti) sur supchains.com
